your pee tested positive for drugs / I AM NOT A DRUG USER! / your pee tested positive / I AM NOT A DRUG USER! / your pee tested positive / I AM NOT A

Hmmm uhhhh this is pretty arcane and obtuse. So I apologize (for bringing back memories of Mrs. Price, your 10th grade Algebra teacher).

Lately people have been describing state lotteries as a Tax on people who are bad at math.

We live in an environment where increasingly, for one bad reason or another bad reason, a private company or government agency or school demands a urine sample from you.

You tinkle while a monitor watches or listens (to make sure you didn't smuggle in a vial of Certified Pure Nun's Urine), and then you wait for a few weeks for the test result.

Someone in a laboratory will make a decision about whether you're a drug user or not. If it's POSITIVE for some illegal substance, a variety of Bad Things will happen to you, and over the next two years you and a lawyer can work out the legal ramifications of that. You may be kicked out of school, or kicked out of the military, or fired, or sent to jail or prison.

But the whole ordeal begins in the laboratory. After the chemistry test, here is precisely how the lab makes its decision about you, and this is a precise computation of the size of the mess or the depth of the shit you're in.

Should you care? Is this more than you want to know or more than you think you need to know? Wouldn't you just rather pee and wait and hope, and ignore everything else?

These are the equations from statistics and probability called Bayes' Theorem, and Wikipedia had this really dandy example, and I wanted to share it with you.

I'm curious to know what you think about it.

I read a lot of whack shit on the Internet, yards of text that seem to make no sense whatsoever.

Here's 8 inches of some whack shit that seems to make no sense whatsoever.

I strongly recommend you crawl to the last paragraph, which is authentically interesting and surprising.

(Did you folks know this? Am I the last to get this news?)

Science historians call World War One "the chemists' war" and World War Two "the physicists' war," and predict World War Three will be "the mathematicians' war" -- that is, the side that does complicated or new math best will win.

This example explains down to the smallest nut and bolt how the lab decides that you're a user of illegal drugs.

================

from Wikipedia

================

Bayes' Theorem

Example #2: Drug testing

Bayes's theorem is useful in evaluating the result of drug tests.

Suppose a certain drug test is 99% accurate, that is, the test will correctly identify a drug user as testing positive 99% of the time, and will correctly identify a non-user as testing negative 99% of the time.

This would seem to be a relatively accurate test, but Bayes's theorem will reveal a potential flaw. Let's assume a corporation decides to test its employees for opium use, and 0.5% of the employees use the drug.

We want to know the probability that, given a positive drug test, an employee is actually a drug user.

Let "D" be the event of being a drug user and "N" indicate being a non-user.

Let "+" be the event of a positive drug test.

We need to know the following:

* Pr(D), or the probability that the employee is a drug user, regardless of any other information. This is 0.005, since 0.5% of the employees are drug users.

* Pr(N), or the probability that the employee is not a drug user. This is 1-Pr(D), or 0.995.

* Pr(+|D), or the probability that the test is positive, given that the employee is a drug user. This is 0.99, since the test is 99% accurate.

* Pr(+|N), or the probability that the test is positive, given that the employee is not a drug user. This is 0.01, since the test will produce a false positive for 1% of non-users.

* Pr(+), or the probability of a positive test event, regardless of other information. This is 0.015 or 1.5%, which found by adding the probability that the test will produce a true positive result in the event of drug use (= 99% x 0.5% = 0.495%) plus the probability that the test will produce a false positive in the event of non-drug use (= 1% x 99.5% = 0.995%).

Given this information, we can compute the probability that an employee who tested positive is actually a drug user:

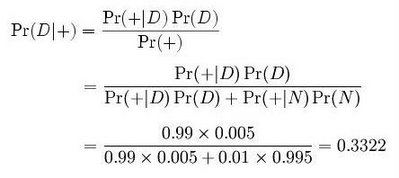
Despite the high accuracy of the test, the probability that the employee is actually a drug user is only about 33%. The rarer the condition for which we are testing, the greater percentage of the positive tests will be false positives. This illustrates why it is important to do follow-up tests.