


I sincerely hope this wiggles for you.
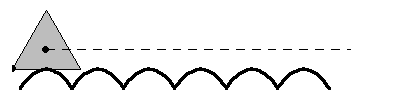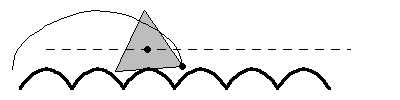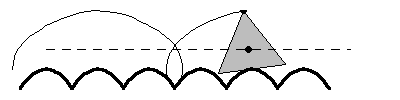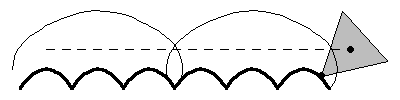
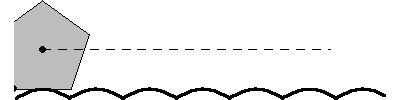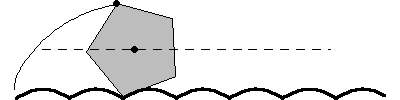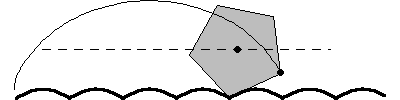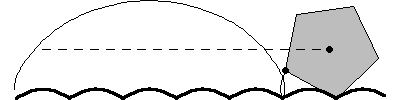
A regular n-sided polygon (all side lengths and interior angles equal) can roll smoothly along a road -- technically called a roulette -- composed of a series of identical hump-up catenaries.
A regular polygon rolls as smoothly along its roulette of catenaries as a circle or wheel rolls along a straight line or flat road.
The specific catenary associated with each specific n-sided regular polygon is described by a function of n.
Wigglegifs filched from http://mathworld.wolfram.com , Eric Weisstein's exhaustive and authoritative website of mathematical information. If you're ever in any kind of math jam, go here. Or if you just want to surf some incredibly nifty images and read about some astonishing stuff, you can get really lost in mathworld and someone will have to find you and pull you out. Or send you some clothes.
I am embarrassed to report that in the top equation for designing the catenary for the roulette for a particular n-sided polygon, I don't know what R stands for. I have a query in, I'll let you know as soon as I know.
OKAY I FIGURED OUT
WHAT R STANDS FOR!
WHAT R STANDS FOR!

8 comments:
Ok. That's just cool.
I'm pretty sure that the R you're looking for stands for Roulette, but then my math has never been that good.
no no i *DOH* figured it out finally. It's a very elementary thing with regular polygons.
R is the length of the line from the center to a vertex of the polygon.
small r is the length of the perpendicular from the center to the midpoint of a side.
I'm fixing the diagram now. I'm pretty damn sure I got it right. The diagram is a little hard to draw cause my MS Paint doesn't have a protractor function.
I think R is actually supposed to be half the length of an edge of the wheel. If you wanted R to be as you described it, the distance from the center of the wheel to a vertex, then I think you would need A = R cos(pi/n) instead of A = R cot(pi/n). I apologize if I'm wrong.
Yo Anonymous --
Don'r apologize for trying to set me straight! I'm always grateful for help! I love math, but I ain't exactly Isaac Newton here.
I'll study your definition for R and see if it makes more sense than mine.
So what were you fishing for that got you here? Who are you what are you where are you?
We got an outstanding unanswered Pizza Prize Question that's sort of math-ish, check it out, take a whack at answering it.
http://vleeptronz.blogspot.com/2010/01/pizzaq-line-segment-ac.html
Quite helpful data, lots of thanks for this article.
I found a great deal of helpful info here!
Thanks so much for your article, quite helpful material.
Post a Comment